Louis Kessler’s Behold Blog

It’s always an exciting day when your DNA results come back. After analyzing my uncle’s results ad infinitum for the past six months, I finally bit the bullet and sent away for my own test. The FamilyTreeDNA Holiday Season sale with coupons for extra dollars off was quite motivating.

I ordered my own test on November 14. It arrived on Nov 24 and I did the cheek swabs the next day and mailed it. Yesterday, I got the email that said my results were in.

So these are the Steps I recommend that you do when your autosomal results come in:

Step 1. Don’t Panic! Yes, you can be excited, but take your time and do it right.

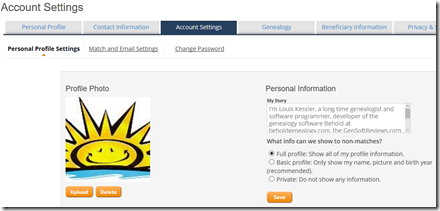
Step 2.   Sign in online to your myFTDNA account. If you haven’t already, do some administrative stuff first. Once your results are there, people are going to find you and you won’t want to look like literally a nobody. Add an “About Me” and image to your Profile.

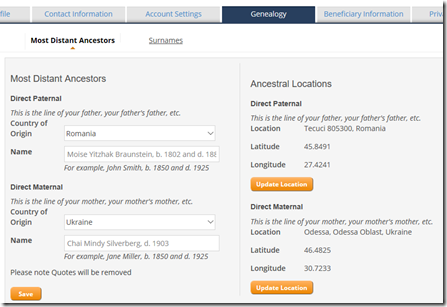
Step 3.   Next to the Account Settings tab is the Genealogy tab. Enter your Most Distant Ancestors:

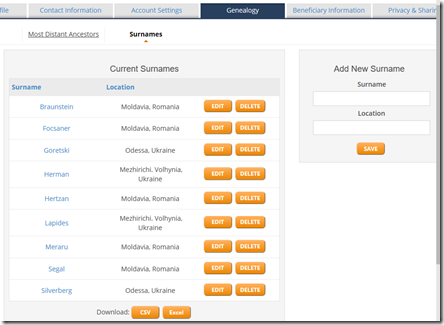
Step 4. Also on the Genealogy tab, enter your Ancestral Surnames:

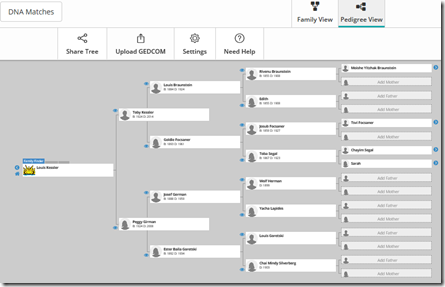
Step 5. Now go to Family Tree and enter your parents, grandparents, great-grandparents, etc.  No need to enter all the details, but make sure you have all your ancestors names, birth years and death years. And I wouldn’t yet enter any other brothers, sisters or children/grandchildren of your ancestors. That gungs things up a bit. There is a better way to add them. See step 11 below.

There. You’re all set up. People can find you and they’ll be able to see if they might share family and by providing this information, you’ve invited them to contact you.

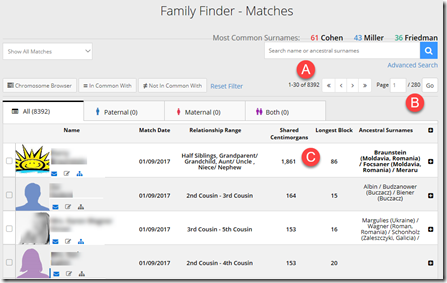
Step 6. Now check out your Family Finder results. Go to the matches page and, if you’re like me and are from an endogamous population, prepare to be overwhelmed.

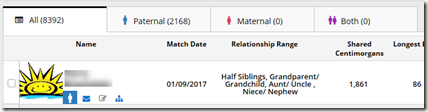
You’ll see you have (A) 8,392 people who match you, and it will take (B) 280 pages to display them. Then (C) check the first few at the top and see if there is any one you know who is a relative.

Step 7.   Either breathe a sigh of relief when you see your uncle shares 1,861 cM as he should, or agonize a bit … maybe a lot .. as you search desperately for your uncle in the list. You know he tested. If he’s not there, then go back to step 1, except now you Panic!

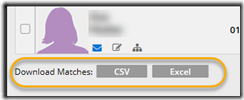
Step 8. You don’t want to go through the Family Finder matches one-by-one. There’s a better way. Download your matches. At the bottom of the Family Finder matches page, there are two buttons:  CSV or Excel

CSV is a comma delimited text format. Excel isn’t really Excel but is XML. It doesn’t matter which one you use. They both contain the same information. And Excel or any spreadsheet software can read them both. I usually use CSV, so hit the CSV button and download the file.  It will be called something like: nnnnnn_Family_Finders_Matches_yyyymmdd.csv.

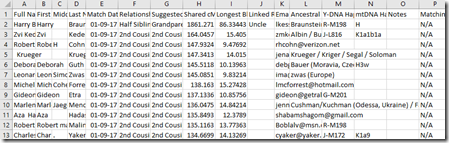
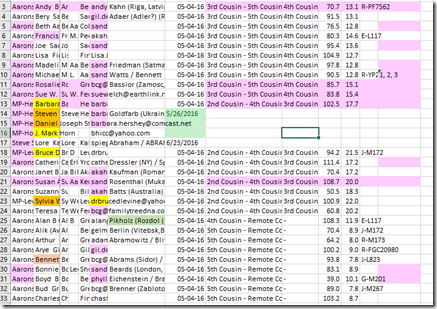
Step 9. Open that file in Excel or your spreadsheet software. Right away save the file with a meaningful name and in the format of your spreadsheet software (e.g. Excel is .xlsx) so that all the spreadsheet features will be retained. I named my file “LK Master Match List.xlsx”. Your file should look like this:

… and yes, they are scrunched just about that much.

The key thing here is that you’ve got all your match data and it is much easier to sort or search or highlight or add your notes in a simple spreadsheet than trying to do so on the FamilyTreeDNA site.

The columns include:
- Full Name
- First Name  (You can delete this, as it’s superfluous)
- Middle Name (This too)
- Last Name (You’ll need this to sort by last name)
- Match Date
- Relationship Range
- Suggested Relationship (I’d hide this. Relationship Range is good enough)
- Shared cM
- Longest Block (Change title to: Max cM)
- Linked Relationship
- Email (I’d move this after the Name)
- Ancestral Surnames
- Y-DNA Haplogroup
- mtDNA Haplogroup
- Notes
- Matching Bucket

The one field that FamilyTreeDNA does not include that I feel is important, that 23andMe includes in their match download file, is the person’s Sex. Oh well, we won’t worry about that for now.

Step 10.   Now go through all your matches in your list of 8,392 and make a note of anyone who is already a known relative of yours. Other than my uncle, I had a 3rd cousin Joel. He and I have been sharing our research on our common line for about 15 years. So I’ve got my Uncle, whose test I submitted, and Joel. That’s it. 2 out of 8,392. Maybe you have more.

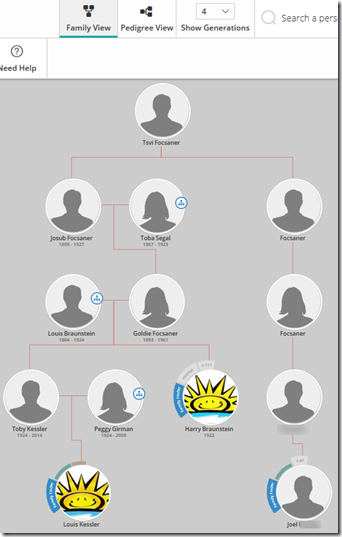
Step 11.   It’s time to go back to your Family Tree at FamilyTreeDNA and add your known relatives. For my uncle, I would add him as a son to my grandfather. For my third cousin Joel, I would find our common great-great grandparents, add a son, add a daughter to the son, add a son to the granddaughter, and add Joel under the great-grandson. Don’t bother naming the people in-between.

Doing this will not only let you get a picture of where your relatives are in your DNA tree, but it will also get the FamilyTreeDNA site to start calculating something pretty cool for you. It’s going to use the DNA matches of your relatives to figure out for all your 8.392 people, who matches you on your father’s side, who matches you on your mother’s side, who on both sides, and who matches but the side isn’t determined yet. You’ll then see this on your matches page:

Both my uncle and Joel are on my father’s side, so it has figured out that 2,168 of my 8,392 matches also match to either my uncle or Joel. And now those little symbols for paternal, maternal , or both , will be shown alongside each of your matches to which they apply.

Step 12.   With that bit of extra information, download your Family Finder matches again (see Step 8). This time, that last field called “Matching Bucket” will be loaded with Paternal or Maternal or Both or N/A.

Step 13.   Now go at it and have fun. Look in your spreadsheet for people you know, your ancestral surnames, anything that looks interesting. Use the Notes column for your thoughts on this match. Color code people that are of interest to you. Add other columns as you see fit. If you don’t end up with something pretty like this, then you’re doing it wrong:

Step 14.   If you made it all the way here, that’s super!

Now you should be daring. Contact the DNA relatives you don’t know who you might be able to figure out a relationship to, and your DNA adventure will begin. You’ll be consumed by it.

Update: January 16, 2017. Contest Winner Chosen.

My daughter did the random stuff and pulled the name out of the hat (actually it was a plastic bag)

The lucky winner was:  Carole Steers

Congratulations, Carole

Here is maybe your last chance to get a RootsTech/Innovator Showdown 4-day pass for free, a $299 USD value.

Personally, I’m really looking forward to RootsTech. I was there twice before, in 2012 and 2014 and it was fantastic each year. This year, I was one one of the 40 entrants in the Innovator Showdown. I entered my program Double Match Triangulator (DMT), a Windows program for autosomal DNA analysis. My program was selected as one of the 10 semi-finalists in the contest and I’ll be pitching it live at RootsTech, in a Shark-Tank-like format, on Wednesday February 8, the Innovator Summit day of RootsTech.

Each of the RootsTech Ambassadors were given a free pass to give away. I’m not an Ambassador, but I was given an extra pass that I am allowed to give to someone.

To enter my giveaway, send me an email* at: lkessler@lkessler.com and to qualify, include a weblink that will take you directly to my Double Match Triangulator page on this (my beholdgenealogy.com) website. It shouldn’t be too hard to find.

*Your email address will be kept private and you won’t be added to any lists.

The winner will be chosen randomly from the entrants with a correct weblink.

Good luck. This Giveaway closes one week from today, on Monday January 16, 2017 at 2:00 p.m. CST.

Yesterday was 20 years from the day I put up my first official web pages in 1997. (Rats. I missed it. I should have had my web-iversary in my appointment calendar.)

I started webhosting using the services of Concentric.net who in 2000 were acquired by XO. My original web address was: www.concentric.net/~lkessler. The next year, 1998, I acquired my lkessler.com domain, when there were still some 8 letter .com domain names available.

My site started with several pages. I’ve recovered the earliest of my original pages from the Internet Archive:

This was my personal home page, as of January 25, 2000, which is about as far as the Internet Archive goes back:

At that time, I was interested in Internet searching and was working on a desktop tool I was calling Alli-getter to do that. Google search was not launched until February 2002, so this was pre-Google, when good tools were needed for searching. I ended up not completing that and spent my spare time working on Behold instead.

I had several other pages up there as well on my initial launch. They included:

1. My Genealogy Pages (snapshot from Feb 17, 2001)

2. My Family Research page (snapshot from Aug 18, 2000)

3. My writeup of our Society’s Cemetery Photography Project. Back then, we did it with real film. (Snapshot from Aug 18, 2000)

4. A primer for newbees to genealogy research (Aug 18, 2000)

5. A home page for my genealogical society. (Oct 4, 1999)

6. A page for my society’s Genealogical Institute (Dec 17, 1999)

7. A search page of surnames in our Society’s database (Sept 3, 2000)

8. My Stars, a page for my family’s interests (Feb 14, 2001):

9. Your Last Stop, a page to remind me of Cheryl’s constant message to me (Feb 18, 2000):

10. As well as the first cut of my Behold page, with the ideas simmering in my mind and several years before the first alpha release (snapshot Dec 28, 2002)

All of those pages, except My Stars (which I merged into my lkessler.com home page) still exist. You can click on the above pictures to see what they look like today.

My original host Concentric used Windows servers, and I did some scripting using ASP (Active Server Pages), the Windows scripting language, to add some dynamics to my pages, e.g. redirection and page counting. The ASP pages required a .shtml extension with the “s” telling the server to preprocess the pages with ASP. That is the reason all my pages today on lkessler.com are still .shtml as I haven’t bothered to change the suffix to .html or .htm or .php.

In April 2000, when Concentric was sold, I left them for myhosting, a Canadian company. By about 2006, myhosting was not being all that great a host and I moved beholdgenealogy.com, gensoftreviews.com and jhcwc.org to IXWebhosting. They too did not work out at all, so in January 2009, I moved all my sites to Netfirms where they are today. That’s 4 webhosts in 20 years. Let me tell you, transferring is a pain, so don’t do it unless it’s necessary.

I’ve added lots of content to my pages over the years. I’m proud of what I’ve assembled which is a lot. I customized everything about my sites to be what I want, including hacking into the PHP code of Wordpress and bbPress to make my Behold blog and forum as well as GenSoftReviews be exactly what I wanted them to be.

The first web editor I used was HomeSite, developed in 1995 by Nick Bradbury. It was designed for direct editing, or “hand coding” of HTML. I liked it also because it Nick wrote it in Delphi, the programming language I used and still use. When Allaire Corporation acquired HomeSite from Nick, he started work on TopStyle and later I switched to it. TopStyle was acquired from Nick in 2008, but I still use it today. Sometime last year, the new owners of TopStyle stopped supporting it and the site is gone today. I will likely have to switch to another product to maintain my sites. But TopStyle is still doing the job for me today, so I can hold off on that a bit.

I’ve made lots of changes to my websites over the years. And I’ve maintained a log of all the major changes I’ve made to the site over the past 20 years on my What’s New page.

20 years! Yes, it seems that long!